Das Lineal als Gitarre
Aus unserem Lineal kann man ganz einfach ein Musikinstrument bauen. Man benötigt dafür nur das Lineal, ein Gummiband und einen Stift.

Man umspannt das Lineal mit dem Gummiband und legt den Stift zwischen Lineal und Gummiband. Durch Verschieben des Stiftes kann nun die Länge der schwingenden Saite eingestellt werden. Diese ist maßgeblich für die hörbare Tonhöhe verantwortlich.

Den schönsten Ton erhält man, wenn man mit einer Hand den Auflagepunkt des Gummibands auf dem Stift fixiert und mit der anderen Hand die Gummi-Saite zum Schwingen bringt.

Möchte man herausfinden, welcher Ton bei einer bestimmten Position des Stiftes zu hören ist, kann man dies zum Beispiel mit der phyphox-App bestimmen. Hierfür wählt man in der App den Menüpunkt „Frequenz-Verlauf“ aus und tippt auf das Frequenz-Diagramm, um eine vergrößerte Darstellung zu erhalten. Sobald man auf den „Play-Button“ drückt beginnt die Messung.
(Die QR-Codes führen zum Download der phyphox-App.)
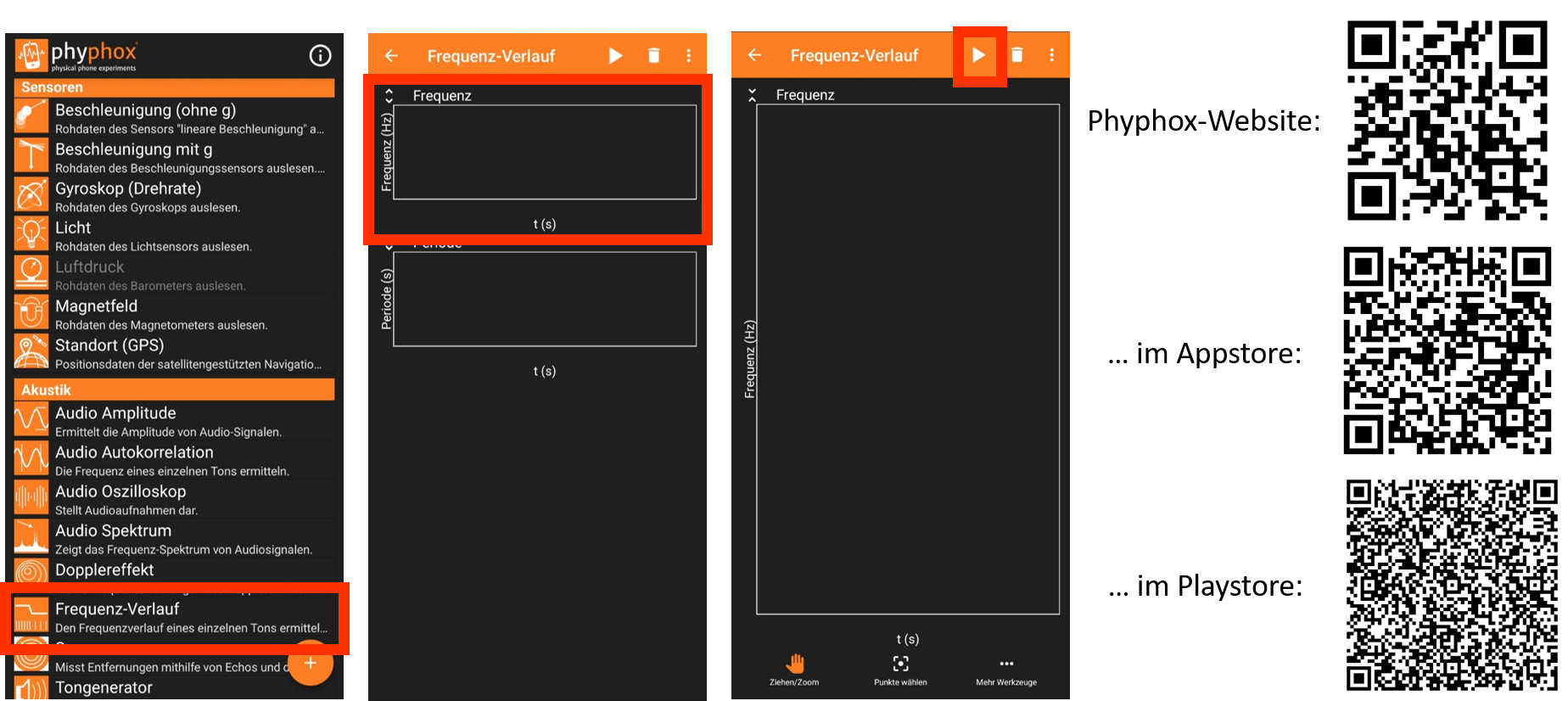
Nun muss man solange die Saite zupfen, bis sich genügend Messpunkte bei einer Frequenz gesammelt haben. Das Mikrofon des Smartphone nimmt auch alle anderen Geräusche im Raum auf, wodurch viele verschieden Frequenzen gleichzeitig gemessen werden.
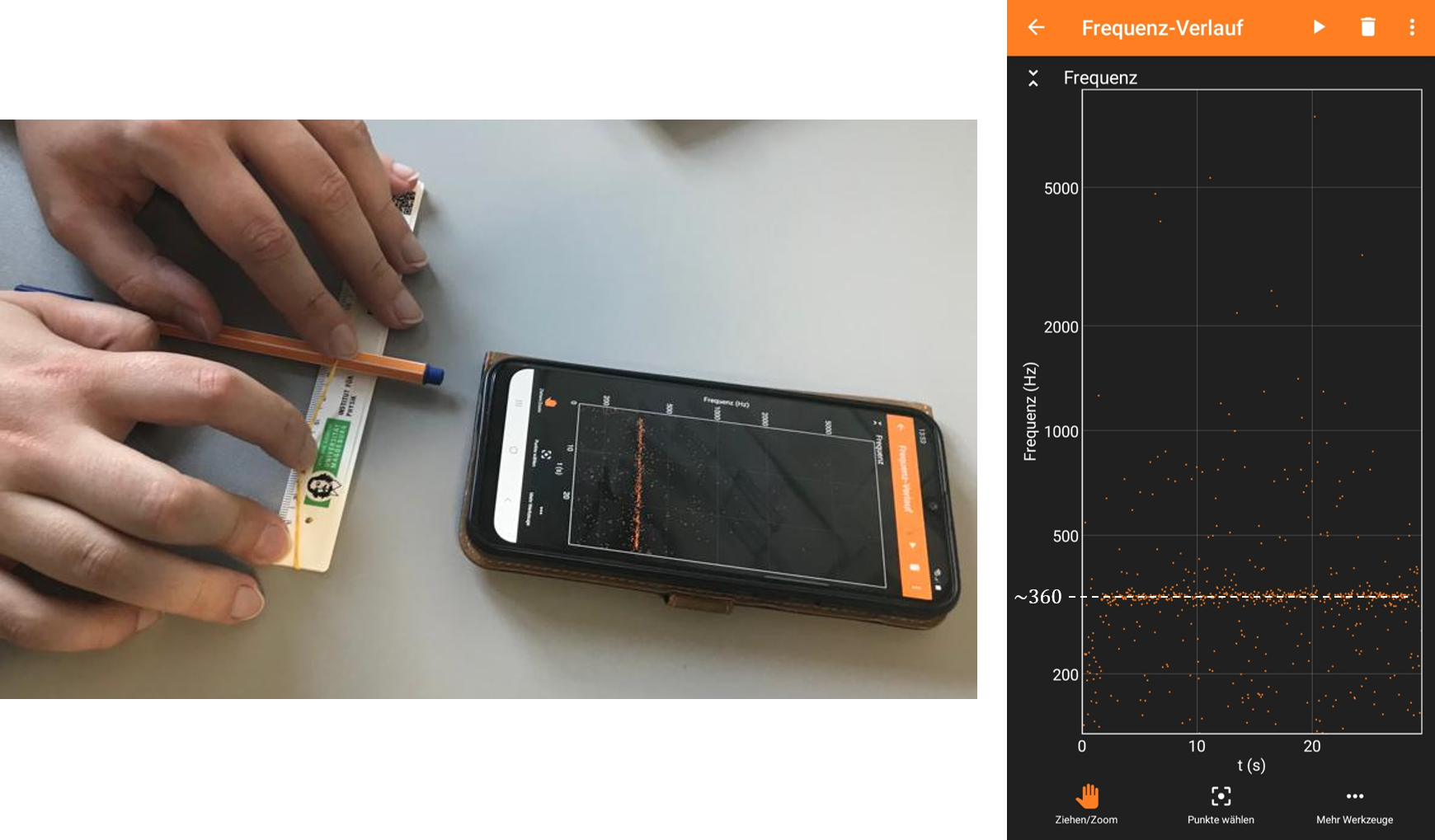
Die Frequenz der schwingenden Saite hängt von drei Parametern ab: der Länge L der Seite , der Spannung σ der Saite und der Dichte des Materials der Saite ρ. In diesem Experiment nehmen wir an, dass sich die Spannung und die Dichte der Saite nicht signifikant verändern.

Man kann nun mithilfe der phyphox-App die entstehenden Frequenzen bei verschiedenen Positionen des Stiftes aufnehmen. Da der Frequenzverlauf jedoch nur zeitlich angezeigt wird, sollte man sich gut merken in welchen Abständen man den Stift positioniert hat.
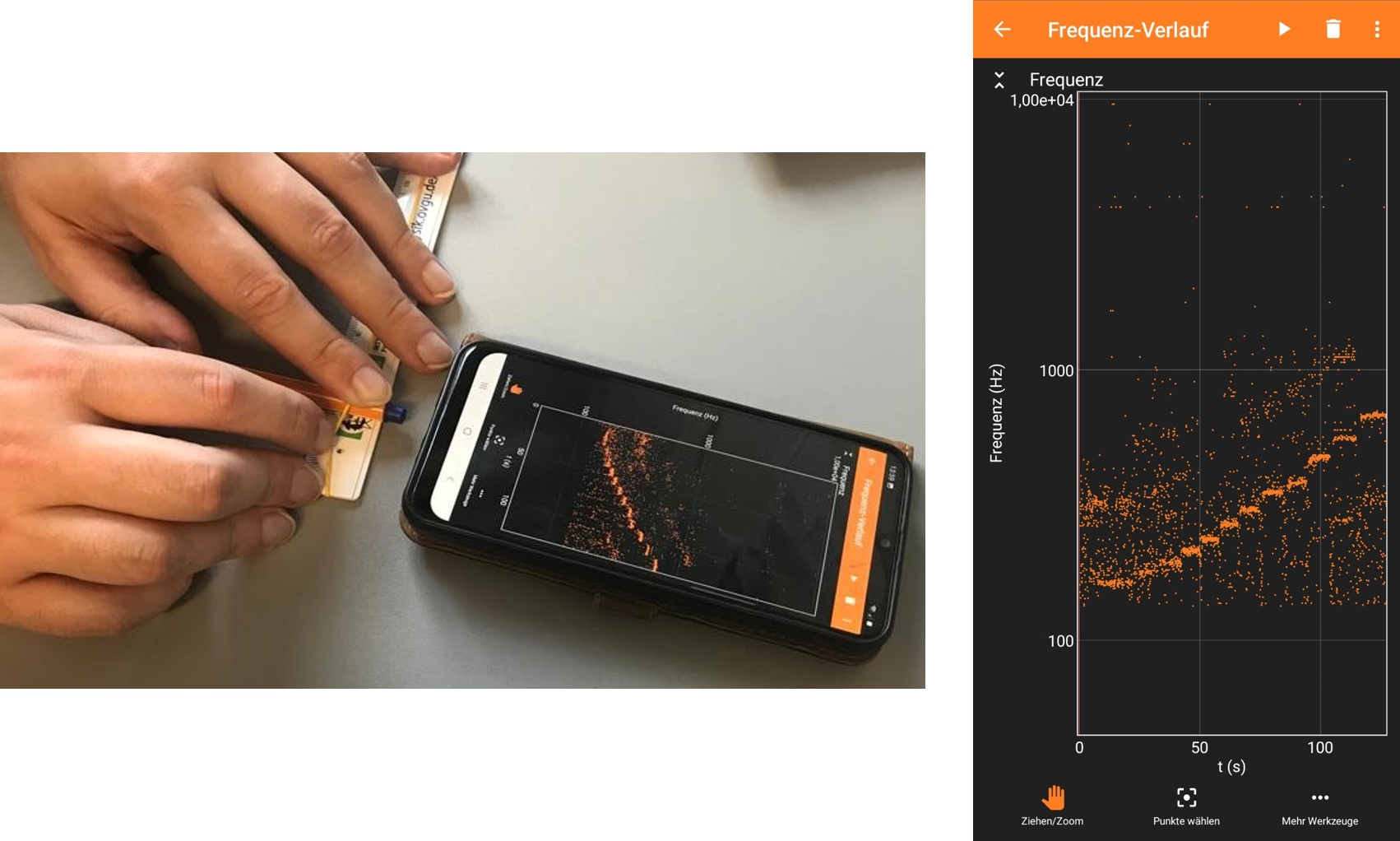
Jetzt kann man die gemessenen Frequenzen als Funktion der Position des Stiftes darstellen. Man muss aber beachten, dass die Position des Stiftes (z.B. am 5 cm-Teilstrich) nicht der Länge der Saite entspricht. Hierfür müssen wir den Satz das Pythagoras verwenden und die Höhe des Stiftes zusätzlich kennen und berücksichtigen.
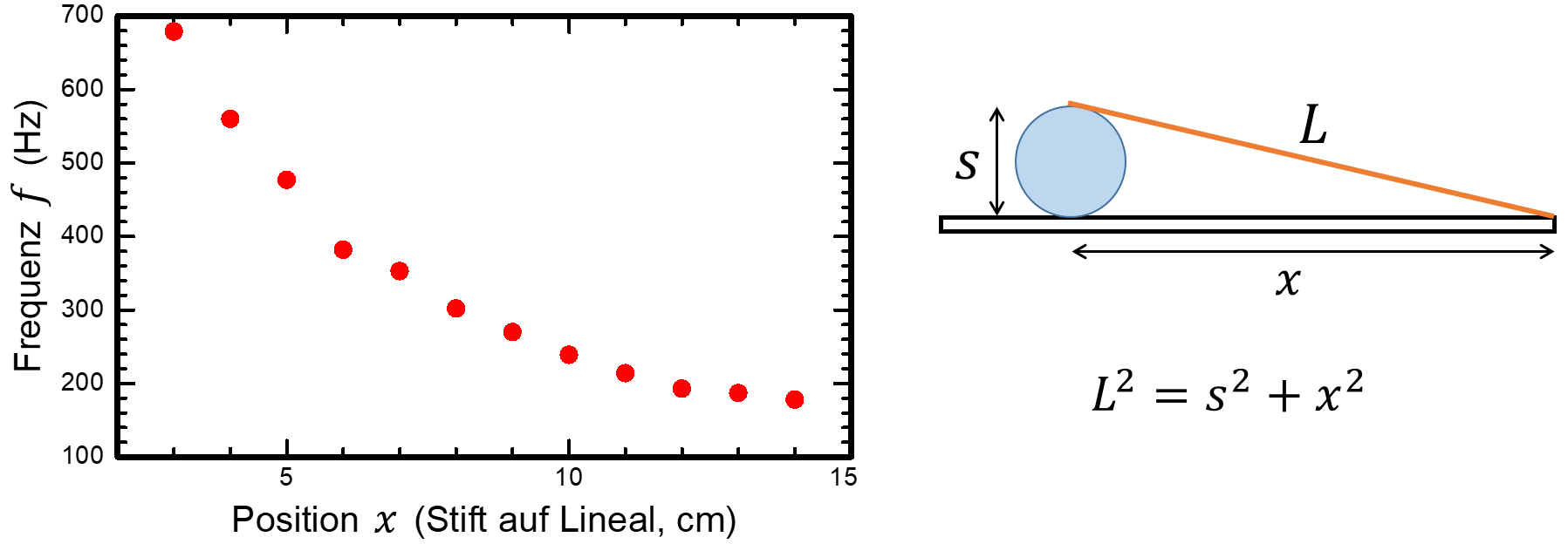
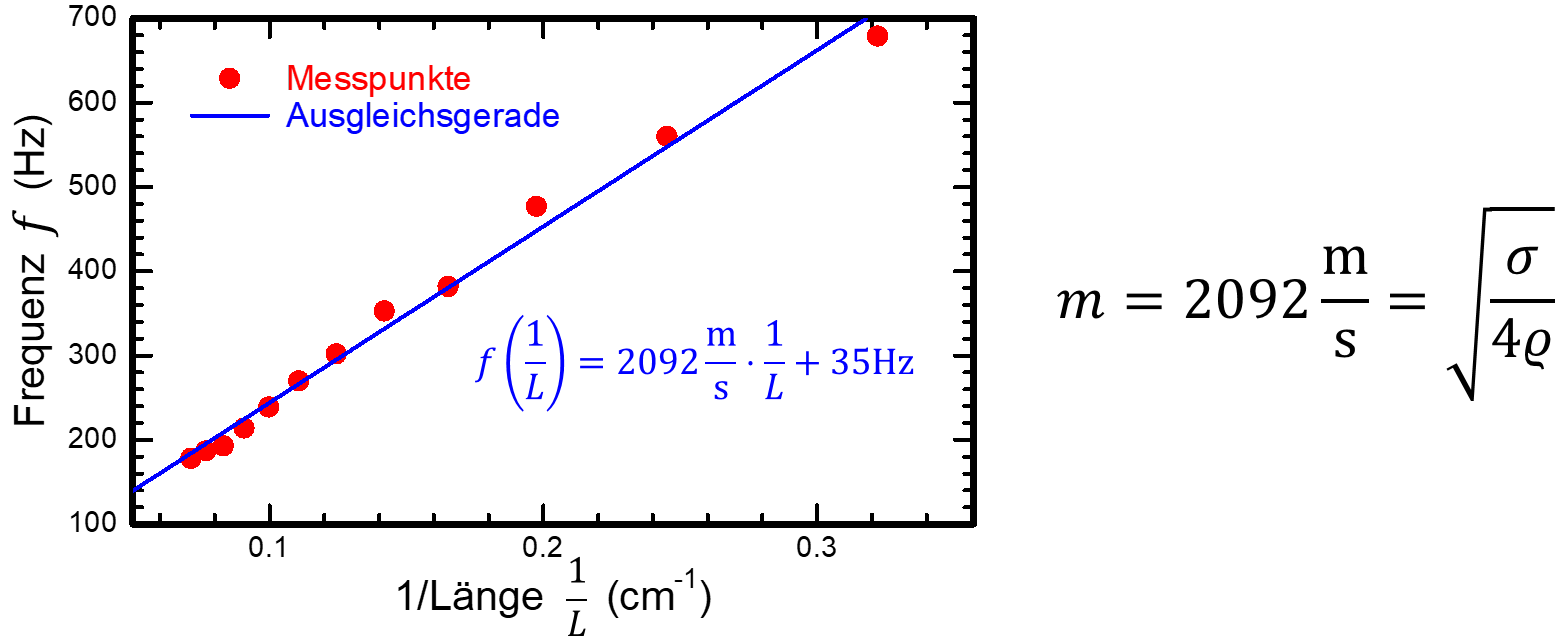
Für eine korrekte Auswertung stellt man jetzt die gemessene Frequenz über 1/L dar. Es ergibt sich ein linearer Zusammenhang und man kann eine Gerade durch die Messpunkte legen. Der Anstieg m dieser Geraden entspricht √(σ/(4ρ)). Wenn die Dichte bekannt ist, kann also die Spannung des Gummibandes berechnet werden.
Man könnte nun noch zusätzlich die Spannung auf das Gummiband erhöhen, indem man einen zweiten Stift benutzt um das Gummiband zu verdrehen. Durch die veränderte Spannung ergeben sich verschiedene Anstiege der Ausgleichsgeraden.
